【新】バランス理論の数式表現 その9(返報性)
二者間の好悪感情は三者間のバランス理論の他に二者間の返報性がある。
自分のことを好きな人を好きになることはできるが、自分のことを嫌っている人を好きになるのは難しい。自分のことを愛してくれる人のことは愛しやすいが、自分のことを憎んでいる人のことを愛するのは難しい。お中元やお歳暮をもらうと自分もお中元やお歳暮を贈らないといけないような気になる。プレゼントをもらうとプレゼントを返さないといけないような気になる。親切にしてもらうと自分も相手に親切にしたくなる。「好意の返報性」とか「互恵性」とか呼ばれる有名な心理である。
a が b に好意を示す(ΔWab > 0)と b は a に好意を返す(ΔWba > 0)傾向がある。ただし、b が a から好意を受け取ったと思わない(ΔWab|b ≦ 0)と b は a に好意を返そうとは思わない(ΔWba|b ≦ 0)。a から好意を受け取ったと b が思う(ΔWab|b > 0)と、b は a に好意を返そうと思う(ΔWba|b > 0)だろう。
式で表すと次のようになると思われる。
ΔWba|b = ΔWab|b ……(1)
ΔWab|a = ΔWba|a ……(2)
「=」としたのは、通常は受け取った好意以上の好意を返そうとは思わないだろうし、受け取った好意以下の好意で済まそうともしないと考えられるからである。「ΔWab|a < ΔWba|a」だと a は b に申し訳ないような気になるだろうし、「ΔWab|a > ΔWba|a」では a は損をした気になるだろう。だから a はできるだけ「ΔWab|a = ΔWba|a」となるようにするだろう。相手の好意と同程度の好意を返す。ギブアンドテイクである。
ただし、「ΔWab|b = ΔWab|a」とは限らないから注意が必要である。a が b に喜ぶと思って贈ったプレゼントが、b にとっては嬉しくないものかもしれない。
(好意の返報性、悪意の返報性)
好意の返報性を一時的な行為と考えるか好悪感情の状態と考えるかで表記が異なるだろう。一時的な行為であれば上記引用のように ΔWab だが、好悪感情の状態であれば Wab(t) が良いと思われる。
ここでは好悪感情の状態として、好意の返報性をバランス理論の数式表現を用いて表してみる。
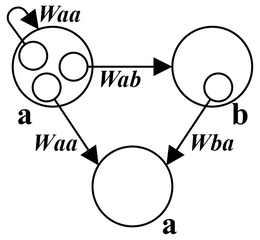
これまでハイダーのバランス理論を数式表現する際に、例えばaのbに対する好悪感情の荷重は次の式を仮定した。
\( \begin{cases} W_{ab}(t+dt) = \dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1)\\ \\ W_{ab}(t+dt) = \dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(2)\\ \\ W_{ab}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1')\\ \\ W_{ab}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(2')\\ \end{cases} \)
式(1)は「aはcが好き。cはbが好き。だからaはbが好き」というバランスを表したもので、式(2)は「aはcが好き。bもcが好き。だからaはbが好き」というバランスを表したものである。この式(2)のcをaに置き換えることで好意の返報性を表せるのではないかと思われる。
\( \begin{align} W_{ab}(t+dt) &= \dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{aa}(t) \cdot W_{ba}(t)}{|W_{aa}(t)| + |W_{aa}(t)|}\\ \\ &= \dfrac{W_{aa}(t)}{|W_{aa}(t)|} \cdot \dfrac{W_{ab}(t) + W_{ba}(t)}{2}\\ \\ &= \dfrac{W_{ab}(t) + W_{ba}(t)}{2}\cdots(W_{aa}(t)>0)\cdots(3)\\ \\ &= - \dfrac{W_{ab}(t) + W_{ba}(t)}{2}\cdots(W_{aa}(t)<0)\cdots(4)\\ \end{align} \)
式(2')のcをaに置き換えると次のようになる。
\( \begin{align} W_{ab}(t+dt) &= \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{aa}(t) \cdot W_{ba}(t)}{|W_{aa}(t)| + |W_{aa}(t)|}\\ \\ &= \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{aa}(t) \cdot W_{ba}(t)}{2 \cdot |W_{aa}(t)|}\\ \\ &= \dfrac{W_{ab}(t) + W_{ba}(t)}{2}\cdots(W_{aa}(t)>0)\cdots(3')\\ \\ &= \dfrac{W_{ab}(t) - W_{ba}(t)}{2}\cdots(W_{aa}(t)<0)\cdots(4')\\ \end{align} \)
【新】バランス理論の数式表現 その8(荷重が0になる件の再考察)
【新】バランス理論の数式表現 その3(3人の相互作用)では、ハイダーのバランス理論を数式表現する際に次の式(1)~(6)を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(3)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(5)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(6)\\ \end{cases} \)
【新】バランス理論の数式表現 その7(もう一つの式)では、ハイダーのバランス理論を数式表現する際に次の式(7)~(12)を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(7)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(8)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(9)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(10)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(11)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(12)\\ \end{cases} \)
初期状態を Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1 にすると、それぞれの荷重は式(1)~(6)では次の図1のように変化し、式(7)~(12)では図2のように変化する。
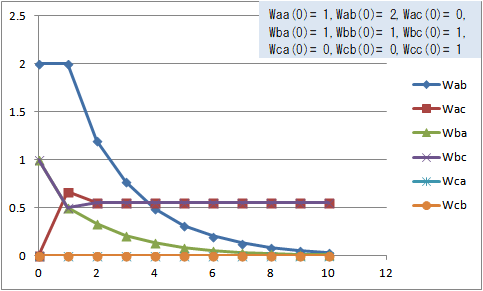
図1 式(1)~(6)での荷重の変化(Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1)
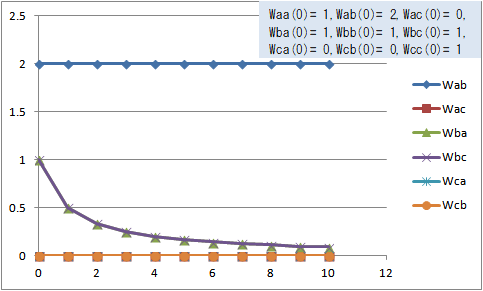
図2 式(7)~(12)での荷重の変化(Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1)
cの影響を排除するために Wca(0)=0, Wcb(0)=0 としたのだが、式(1)~(6)では Wab(t) と Wba(t) が0に収束し(図1)、式(7)~(12)では Wac(t) が0のままで Wbc(t) は0に収束した(図1)。
これは、式(1)~(6)、式(7)~(12)は Wca(0)=0, Wcb(0)=0 とすると、次の式(13)~(18)、式(19)~(24)のようになるため、当然の結果である。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(13)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(14)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(15)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(16)\\ \\ W_{ca}(t+dt) =W_{ca}(t)=0\cdots(17)\\ \\ W_{cb}(t+dt) =W_{cb}(t)=0\cdots(18)\\ \end{cases} \)
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(19)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(20)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(21)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(22)\\ \\ W_{ca}(t+dt) =W_{ca}(t)=0\cdots(23)\\ \\ W_{cb}(t+dt) =W_{cb}(t)=0\cdots(24)\\ \end{cases} \)
式(13)では Wac(t) が0にならない限り、Wab(t+dt) は0に近づく。
式(15)では Wbc(t) が0にならない限り、Wba(t+dt) は0に近づく。
式(20)では Wab(t) が0にならない限り、Wac(t+dt) は0に近づく。
式(22)では Wba(t) が0にならない限り、Wbc(t+dt) は0に近づく。
そして、Wab(t), Wba(t), Wac(t), Wbc(t) がいったん0になると、Wab(t+dt), Wba(t+dt), Wac(t+dt), Wbc(t+dt) は0のままである。その様子が、図1、図2に現れている。
【新】バランス理論の数式表現 その7(もう一つの式)

ハイダーのバランス理論では「好きな人が好きなものが好き」などのように、a、b、cの関係でaからbへの思い( Wab(t) )とbからcへの思いで( Wbc(t) )でaからcへの思い( Wac(t+dt) )が決まるようなパターンの他に、「好きなものが同じだから好き」のように、aからcへの思い( Wac(t) )とbからcへの思いで( Wbc(t) )でaからbへの思い( Wab(t+dt) )が決まるパターンもある。
これまでの記事では、前者の数式を仮定してきた。
- 【新】バランス理論の数式表現 その1(単純な積ではダメ)
- 【新】バランス理論の数式表現 その2(自分の評価も考慮)
- 【新】バランス理論の数式表現 その3(3人の相互作用)
- 【新】バランス理論の数式表現 その4(自分の評価も考慮:修正案)
- 【新】バランス理論の数式表現 その5(3人の相互作用:修正案)
ここでは後者のパターン(「同じものが好きだから好き」など)を次の(1)~(6)の式を仮定して、これまでと同様に各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示す。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(1)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(3)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(4)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{cb}(t)| }\cdots(5)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{ca}(t)| }\cdots(6)\\ \end{cases} \)
また、式(1)~(6)の第1項にある自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がマイナスの場合に符号付きでそのまま反映させるのではなく大きさだけを反映させた次の式(1')~(6')を仮定した場合の各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )の変化についても式(1)~(6)と異なる場合はグラフで示す。
\( \begin{cases} W_{ab}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1')\\ \\ W_{ac}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2')\\ \\ W_{ba}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(3')\\ \\ W_{bc}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4')\\ \\ W_{ca}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(5')\\ \\ W_{cb}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(6')\\ \end{cases} \)
ところで、ハイダーのバランス理論では、次の(A)~(F)の状態では安定で、(G)~(L)の状態では不安定である。そのことを踏まえながら以下の図を見てほしい。
\( \begin{cases} W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) > 0\cdots(A)\\ W_{ab}(t) \cdot W_{cb}(t) \cdot W_{ac}(t) > 0\cdots(B)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) > 0\cdots(C)\\ W_{ba}(t) \cdot W_{ca}(t) \cdot W_{bc}(t) > 0\cdots(D)\\ W_{ca}(t) \cdot W_{ab}(t) \cdot W_{cb}(t) > 0\cdots(E)\\ W_{ca}(t) \cdot W_{ba}(t) \cdot W_{cb}(t) > 0\cdots(F)\\ W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) < 0\cdots(G)\\ W_{ab}(t) \cdot W_{cb}(t) \cdot W_{ac}(t) < 0\cdots(H)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) < 0\cdots(I)\\ W_{ba}(t) \cdot W_{ca}(t) \cdot W_{bc}(t) < 0\cdots(J)\\ W_{ca}(t) \cdot W_{ab}(t) \cdot W_{cb}(t) < 0\cdots(K)\\ W_{ca}(t) \cdot W_{ba}(t) \cdot W_{cb}(t) < 0\cdots(L)\\ \end{cases} \)
【新】バランス理論の数式表現 その6(荷重が0になる件)
【新】バランス理論の数式表現 その3(3人の相互作用)では、ハイダーのバランス理論を数式表現する際に次の(1)~(6)の式を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(1)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(3)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(4)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)| }\cdots(5)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)| }\cdots(6)\\ \end{cases} \)
前回の【新】バランス理論の数式表現 その5(3人の相互作用:修正案)では、ハイダーのバランス理論を数式表現する際に次の(1')~(6')の式を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
\( \begin{cases} W_{ab}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1')\\ \\ W_{ac}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2')\\ \\ W_{ba}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(3')\\ \\ W_{bc}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4')\\ \\ W_{ca}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(5')\\ \\ W_{cb}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(6')\\ \end{cases} \)
式(1)~(6)と式(1')~(6')は第1項の自己評価の荷重をそのまま使うか絶対値を用いて大きさだけを使うかの違いである。【新】バランス理論の数式表現 その5(3人の相互作用:修正案)のグラフを見れば分かるとおり、自己評価の荷重がマイナスの場合はプラスの場合と同じグラフになる。そして、式からも分かるが、【新】バランス理論の数式表現 その3(3人の相互作用)と【新】バランス理論の数式表現 その5(3人の相互作用:修正案)のグラフを比べれば確認できる通り、自己評価の荷重がプラスの場合は式(1)~(6)と式(1')~(6')は同じグラフになる。
そこで、ここでは上の(1)~(6)の式だけを考察する。
【新】バランス理論の数式表現 その3(3人の相互作用)のグラフを見ると荷重が一定の値に収束していることが多い。各荷重が一定の値に収束した時( Wij(t+dt)=Wij(t) )、その値は式(1)~(6)から次のようになる。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{ac}(t) \cdot W_{cb}(t)}{(|W_{aa}(t)| - W_{aa}(t)) + |W_{ac}(t)| }\cdots(7)\\ \\ W_{ac}(t+dt) =\dfrac{W_{ab}(t) \cdot W_{bc}(t)}{(|W_{aa}(t)| - W_{aa}(t)) + |W_{ab}(t)| }\cdots(8)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bc}(t) \cdot W_{ca}(t)}{(|W_{bb}(t)| - W_{bb}(t)) + |W_{bc}(t)| }\cdots(9)\\ \\ W_{bc}(t+dt) =\dfrac{W_{ba}(t) \cdot W_{ac}(t)}{(|W_{bb}(t)| - W_{bb}(t)) + |W_{ba}(t)| }\cdots(10)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cb}(t) \cdot W_{ba}(t)}{(|W_{cc}(t)| - W_{cc}(t)) + |W_{cb}(t)| }\cdots(11)\\ \\ W_{cb}(t+dt) =\dfrac{W_{ca}(t) \cdot W_{ab}(t)}{(|W_{cc}(t)| - W_{cc}(t)) + |W_{ca}(t)| }\cdots(12)\\ \end{cases} \)
自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がプラスの時、式(7)~(12)は次のように簡単な式になる。式(1')~(6')を同様に変形した場合も同じである。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{ac}(t)}{|W_{ac}(t)| } \cdot W_{cb}(t)\cdots(13)\\ \\ W_{ac}(t+dt) =\dfrac{W_{ab}(t)}{|W_{ab}(t)| } \cdot W_{bc}(t)\cdots(14)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bc}(t)}{|W_{bc}(t)| } \cdot W_{ca}(t)\cdots(15)\\ \\ W_{bc}(t+dt) =\dfrac{W_{ba}(t)}{|W_{ba}(t)| } \cdot W_{ac}(t)\cdots(16)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cb}(t)}{|W_{cb}(t)| } \cdot W_{ba}(t)\cdots(17)\\ \\ W_{cb}(t+dt) =\dfrac{W_{ca}(t)}{|W_{ca}(t)| } \cdot W_{ab}(t)\cdots(18)\\ \end{cases} \)
例えば Wac(t+dt) は式(14)により、符号は Wab(t) と Wbc(t) の積で決まってハイダーのバランス理論では安定した状態になり、大きさは Wbc(t) と同じになる。
一方、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がマイナスの時、式(7)~(12)から次のような不等号になることが分かる。
\( \begin{cases} |W_{ab}(t+dt)| < |W_{cb}(t)|\cdots(19)\\ \\ |W_{ac}(t+dt)| < |W_{bc}(t)|\cdots(20)\\ \\ |W_{ba}(t+dt)| < |W_{ca}(t)|\cdots(21)\\ \\ |W_{bc}(t+dt)| < |W_{ac}(t)|\cdots(22)\\ \\ |W_{ca}(t+dt)| < |W_{ba}(t)|\cdots(23)\\ \\ |W_{cb}(t+dt)| < |W_{ab}(t)|\cdots(24)\\ \end{cases} \)
例えば、上の式(20)と(22)を繰り返したら、Wac(t+dt) と Wbc(t+dt) は、お互いの影響で0に近づくことになる。だから、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がマイナスの時は荷重が収束するのなら0に収束するしかない。ただし、一定の値に収束しなかった場合は別の考察が必要である。
式(1')~(6')を同様に変形した場合は式(19)~(24)のような不等号にならず、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がプラスの場合と同じ(13)~(18)の式になる。
ところで、上記は収束した場合の直前の荷重との関係について述べているのであって、最初の各荷重がどのような関係だったら収束するかは述べてないので注意が必要である。
以上を踏まえて、【新】バランス理論の数式表現 その3(3人の相互作用)のグラフで荷重が0に収束しているケースを考察したいのだが各荷重の相互作用があるため変化する荷重が多くて理解しずらいので、変化する荷重を絞った【新】バランス理論の数式表現 その2(自分の評価も考慮)のグラフで、荷重が0に収束しているように見えるケースについて考察する。