【新】バランス理論の数式表現その２（自分の評価も考慮）：【独自研究】ソシオン理論：SSブログ

	ブログをはじめるログイン

【新】バランス理論の数式表現その１（単.. ｜【新】バランス理論の数式表現その３（３.. ブログトップ

【新】バランス理論の数式表現その２（自分の評価も考慮） [編集]

　前回の【新】バランス理論の数式表現その１（単純な積ではダメ）に書いたとおり、ハイダーのバランス理論を数式で表現する際に、次の式(1),(2)のような単純な積では、例えばそれぞれの荷重がプラスの時に値が上昇し続けるなどの問題が生じた。

\( \begin{cases} W_{ac}(t+dt) = W_{ab}(t) \cdot W_{bc}(t) \cdots(1)\\ W_{bc}(t+dt) = W_{ba}(t) \cdot W_{ac}(t) \cdots(2)\\ \end{cases} \)

　そこで、今後は次の(3)～(8)の式を仮定して考察する。

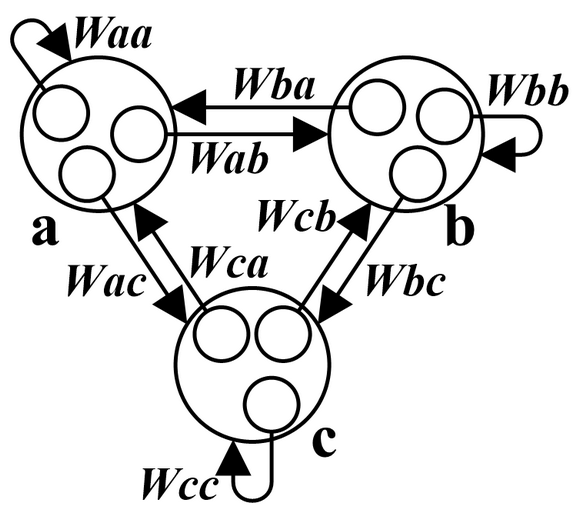
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(3)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(4)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(5)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(6)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)| }\cdots(7)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)| }\cdots(8)\\ \end{cases} \)

　もともとの自分の評価を考慮した式で、例えば、全ての荷重がプラスの場合、Wac(t+dt)ではｃの影響がない時はａのもともとの自分の評価Wac(t)とｂの評価Wbc(t)の間に変化するようになっていて、単純な中間ではなくａの自己評価Waa(t)とａが評価するｂの荷重Wab(t)の大きさの違いによってWac(t)よりになったりWbc(t)よりになったりする。
　上の(3)～(8)の式では三者ａ、ｂ、ｃが影響し合って変化して解釈が難しいので、まずは次のような一部の荷重が変化しないように仮定して試してみる。

\( \begin{cases} W_{ab}(t+dt) = W_{ab}(t) \cdots(9)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(10)\\ \\ W_{ba}(t+dt) = W_{ba}(t) \cdots(11)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(12)\\ \\ W_{ca}(t+dt) = W_{ca}(t) \cdots(13)\\ \\ W_{cb}(t+dt) = W_{cb}(t) \cdots(14)\\ \end{cases} \)

　最初の荷重を Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は次の図１のように変化する。

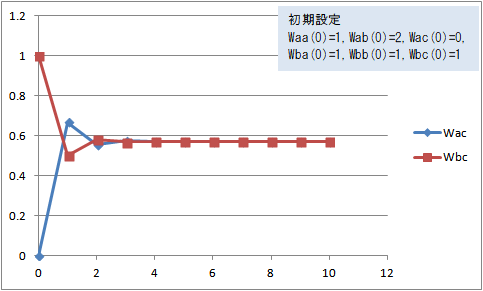
図１ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1）

　Wac(t) と Wbc(t) は近づいて、一時は逆転するが、共に 0.571429 に収束した。

　最初の荷重を Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は次の図２のように変化する。

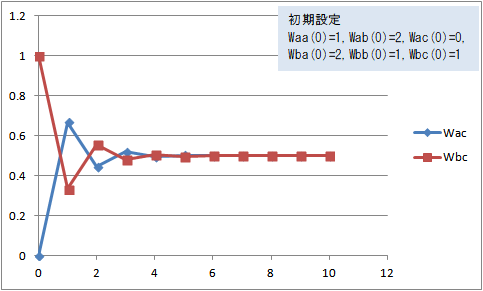
図２ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1）

　図１と変えたのは Wba(0) で、図１では Wab(0) よりも小さい 1 だったが、図２では同じ 2 にしてみた。
　図１よりも収束が遅れて、Wac(t) と Wbc(t) は Wac(0) と Wbc(0) のちょうど中間の 0.5 に収束した。図１ではｂよりａの方が相手に対する思いが強かったのでｂの評価の方に近づいたが、図２では、双方の思いが同じ強さだったのでちょうど中間になったようなイメージである。
　ただし、図１も図２もそれぞれの自己評価が 1 で同じ（ Waa(0)=1, Wbb(0)=1 ）である。これをａの自己評価を高くする（ Waa(0)=10 ）と次の図３のように、もともとのａの評価（ Wac(0)=0 ）に近づいて 0.2 に収束した。

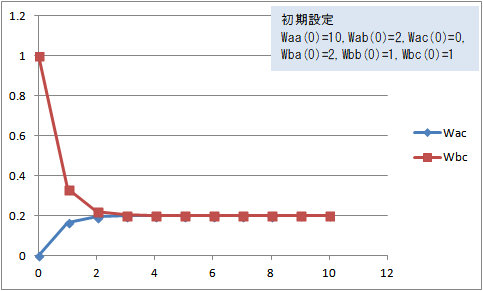
図３ Wac(t)、Wbc(t)の変化（Waa(0)=10, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1）

　次に、一部の荷重をマイナスにしてみる。

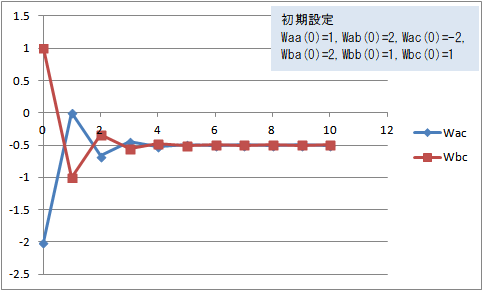
図４ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=2, Wac(0)=-2, Wba(0)=2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=2, Wac(0)=-2, Wba(0)=2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は -0.5 に収束した。

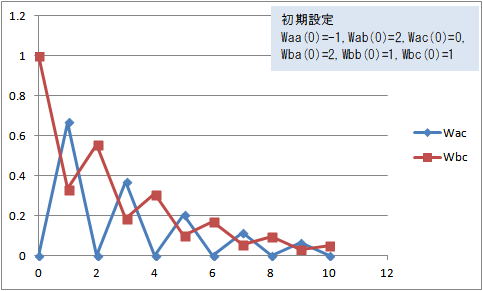
図５ Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は荷重の大きさの逆転を繰り返して０に近づいてる。

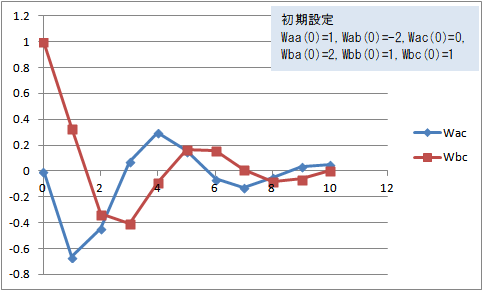
図６ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) はマイナスに振れながら０に近づいてる。

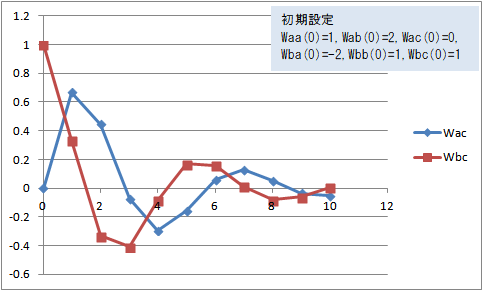
図７ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) はマイナスに振れながら０に近づいてる。

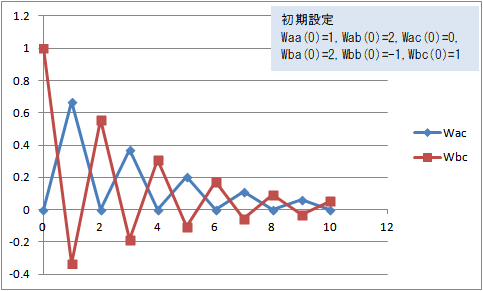
図８ Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は荷重の大きさの逆転を繰り返して０に近づいてる。Wbc(t) はマイナスにも振れてる。

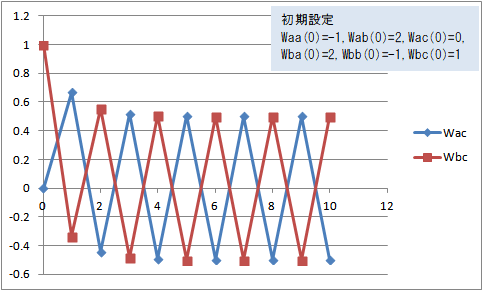
図９ Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は収束することなく荷重の大きさが 0.5 と -0.5 で永遠に逆転を繰り返していそうである。

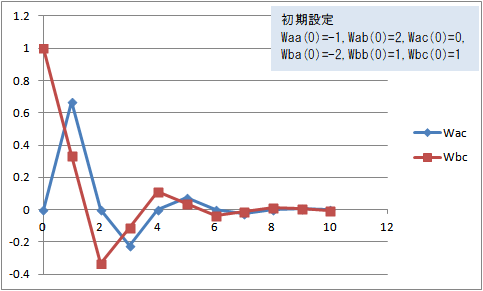
図10 Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) はマイナスに振れながら０に収束した。

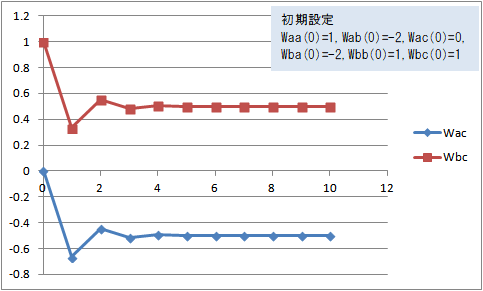
図11 Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) は -0.5 に収束し、Wbc(t) は +0.5 に収束した。

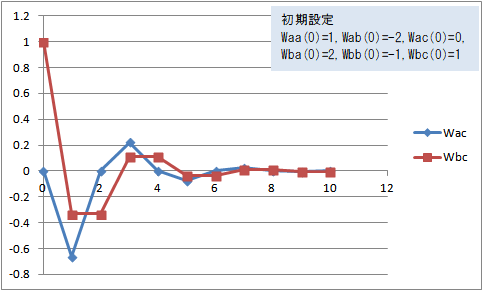
図12 Wac(t)、Wbc(t)の変化（Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1）

　Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) はマイナスに振れながら０に収束した。

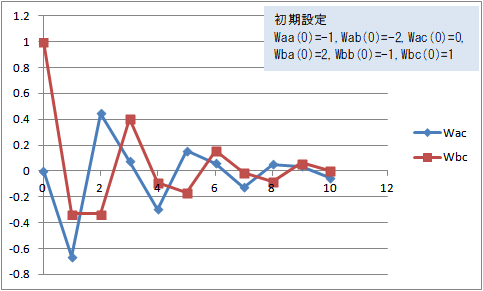
図13 Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) はマイナスに振れながら０に近づいた。

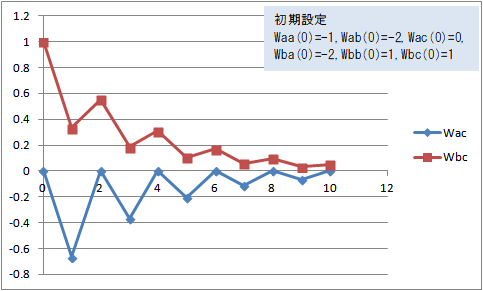
図14 Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は上がったり下がったりしながら０に近づいた。

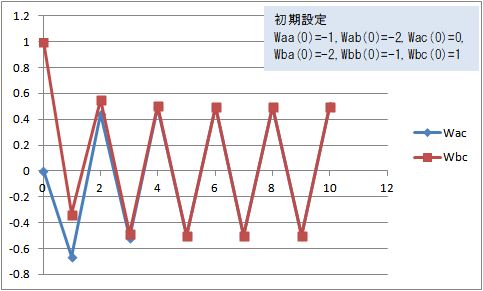
図15 Wac(t)、Wbc(t)の変化（Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=-1, Wbc(0)=1）

　Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=-1, Wbc(0)=1 にすると、Wac(t) と Wbc(t) は荷重の大きさは一致しても収束することなく 0.5 と -0.5 で永遠に振動を繰り返していそうである。

　ハイダーのバランス理論では、次の(A)、(B)の状態では安定で、(C)、(D)の状態では不安定である。そのことを踏まえながら以上の図を見ると良い。

\( \begin{cases} W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) > 0\cdots(A)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) > 0\cdots(B)\\ W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) < 0\cdots(C)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) < 0\cdots(D)\\ \end{cases} \)

　ちなみに自己評価（ Waa(t) 、Wbb(t) ）がマイナスの場合は次のように考えると、常に不安定である。

\( \begin{cases} W_{aa}(t) \cdot W_{ab}(t) \cdot W_{ab}(t) < 0\cdots(E)\\ W_{aa}(t) \cdot W_{ac}(t) \cdot W_{ac}(t) < 0\cdots(F)\\ W_{bb}(t) \cdot W_{ba}(t) \cdot W_{ba}(t) < 0\cdots(G)\\ W_{bb}(t) \cdot W_{bc}(t) \cdot W_{bc}(t) < 0\cdots(H)\\ \end{cases} \)

　次回は、ａ、ｂへのｃの影響を考慮した上の(3)～(8)の式ならどうなるかをグラフで紹介する。

（追記：2022/10/26）
　上の式(3)～(14)の式では自己評価の荷重（ Waa(t) 、Wbb(t)、Wcc(t) ）がマイナスの場合にも同じ式で良いのか疑問が生じたので、修正案を考えました。
　以下の式です。

\( \begin{cases} W_{ab}(t+dt) =\dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(3')\\ \\ W_{ac}(t+dt) =\dfrac{|W_{aa}(t)| \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(4')\\ \\ W_{ba}(t+dt) =\dfrac{|W_{bb}(t)| \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(5')\\ \\ W_{bc}(t+dt) =\dfrac{|W_{bb}(t)| \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(6')\\ \\ W_{ca}(t+dt) =\dfrac{|W_{cc}(t)| \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)| }\cdots(7')\\ \\ W_{cb}(t+dt) =\dfrac{|W_{cc}(t)| \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)| }\cdots(8')\\ \end{cases} \)

　修正案の式よりもこの記事の式の方が良い場合のことを考慮して、この記事は残しますが、修正案でのグラフは後の「【新】バランス理論の数式表現その４（自分の評価も考慮：修正案）」を見てください。