【新】バランス理論の数式表現 その6(荷重が0になる件)
【新】バランス理論の数式表現 その3(3人の相互作用)では、ハイダーのバランス理論を数式表現する際に次の(1)~(6)の式を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
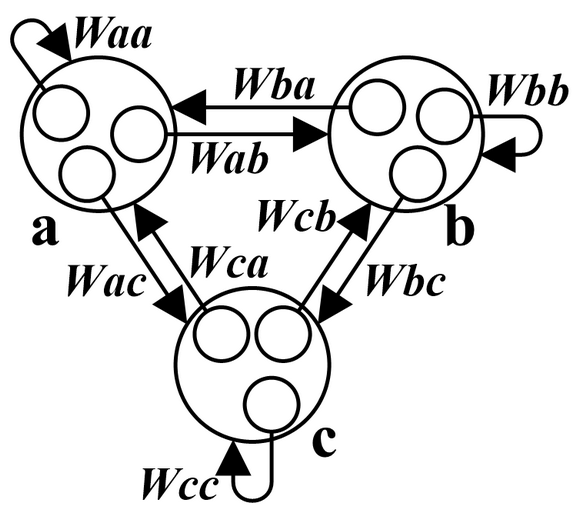
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(1)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)| }\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(3)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)| }\cdots(4)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)| }\cdots(5)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)| }\cdots(6)\\ \end{cases} \)
前回の【新】バランス理論の数式表現 その5(3人の相互作用:修正案)では、ハイダーのバランス理論を数式表現する際に次の(1')~(6')の式を仮定して、各荷重( Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) )がどのように変化するかグラフで示した。
\( \begin{cases} W_{ab}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1')\\ \\ W_{ac}(t+dt) = \dfrac{|W_{aa}(t)| \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2')\\ \\ W_{ba}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(3')\\ \\ W_{bc}(t+dt) = \dfrac{|W_{bb}(t)| \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4')\\ \\ W_{ca}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(5')\\ \\ W_{cb}(t+dt) = \dfrac{|W_{cc}(t)| \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(6')\\ \end{cases} \)
式(1)~(6)と式(1')~(6')は第1項の自己評価の荷重をそのまま使うか絶対値を用いて大きさだけを使うかの違いである。【新】バランス理論の数式表現 その5(3人の相互作用:修正案)のグラフを見れば分かるとおり、自己評価の荷重がマイナスの場合はプラスの場合と同じグラフになる。そして、式からも分かるが、【新】バランス理論の数式表現 その3(3人の相互作用)と【新】バランス理論の数式表現 その5(3人の相互作用:修正案)のグラフを比べれば確認できる通り、自己評価の荷重がプラスの場合は式(1)~(6)と式(1')~(6')は同じグラフになる。
そこで、ここでは上の(1)~(6)の式だけを考察する。
【新】バランス理論の数式表現 その3(3人の相互作用)のグラフを見ると荷重が一定の値に収束していることが多い。各荷重が一定の値に収束した時( Wij(t+dt)=Wij(t) )、その値は式(1)~(6)から次のようになる。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{ac}(t) \cdot W_{cb}(t)}{(|W_{aa}(t)| - W_{aa}(t)) + |W_{ac}(t)| }\cdots(7)\\ \\ W_{ac}(t+dt) =\dfrac{W_{ab}(t) \cdot W_{bc}(t)}{(|W_{aa}(t)| - W_{aa}(t)) + |W_{ab}(t)| }\cdots(8)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bc}(t) \cdot W_{ca}(t)}{(|W_{bb}(t)| - W_{bb}(t)) + |W_{bc}(t)| }\cdots(9)\\ \\ W_{bc}(t+dt) =\dfrac{W_{ba}(t) \cdot W_{ac}(t)}{(|W_{bb}(t)| - W_{bb}(t)) + |W_{ba}(t)| }\cdots(10)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cb}(t) \cdot W_{ba}(t)}{(|W_{cc}(t)| - W_{cc}(t)) + |W_{cb}(t)| }\cdots(11)\\ \\ W_{cb}(t+dt) =\dfrac{W_{ca}(t) \cdot W_{ab}(t)}{(|W_{cc}(t)| - W_{cc}(t)) + |W_{ca}(t)| }\cdots(12)\\ \end{cases} \)
自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がプラスの時、式(7)~(12)は次のように簡単な式になる。式(1')~(6')を同様に変形した場合も同じである。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{ac}(t)}{|W_{ac}(t)| } \cdot W_{cb}(t)\cdots(13)\\ \\ W_{ac}(t+dt) =\dfrac{W_{ab}(t)}{|W_{ab}(t)| } \cdot W_{bc}(t)\cdots(14)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bc}(t)}{|W_{bc}(t)| } \cdot W_{ca}(t)\cdots(15)\\ \\ W_{bc}(t+dt) =\dfrac{W_{ba}(t)}{|W_{ba}(t)| } \cdot W_{ac}(t)\cdots(16)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cb}(t)}{|W_{cb}(t)| } \cdot W_{ba}(t)\cdots(17)\\ \\ W_{cb}(t+dt) =\dfrac{W_{ca}(t)}{|W_{ca}(t)| } \cdot W_{ab}(t)\cdots(18)\\ \end{cases} \)
例えば Wac(t+dt) は式(14)により、符号は Wab(t) と Wbc(t) の積で決まってハイダーのバランス理論では安定した状態になり、大きさは Wbc(t) と同じになる。
一方、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がマイナスの時、式(7)~(12)から次のような不等号になることが分かる。
\( \begin{cases} |W_{ab}(t+dt)| < |W_{cb}(t)|\cdots(19)\\ \\ |W_{ac}(t+dt)| < |W_{bc}(t)|\cdots(20)\\ \\ |W_{ba}(t+dt)| < |W_{ca}(t)|\cdots(21)\\ \\ |W_{bc}(t+dt)| < |W_{ac}(t)|\cdots(22)\\ \\ |W_{ca}(t+dt)| < |W_{ba}(t)|\cdots(23)\\ \\ |W_{cb}(t+dt)| < |W_{ab}(t)|\cdots(24)\\ \end{cases} \)
例えば、上の式(20)と(22)を繰り返したら、Wac(t+dt) と Wbc(t+dt) は、お互いの影響で0に近づくことになる。だから、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がマイナスの時は荷重が収束するのなら0に収束するしかない。ただし、一定の値に収束しなかった場合は別の考察が必要である。
式(1')~(6')を同様に変形した場合は式(19)~(24)のような不等号にならず、自己評価の荷重( Waa(t), Wbb(t), Wcc(t) )がプラスの場合と同じ(13)~(18)の式になる。
ところで、上記は収束した場合の直前の荷重との関係について述べているのであって、最初の各荷重がどのような関係だったら収束するかは述べてないので注意が必要である。
以上を踏まえて、【新】バランス理論の数式表現 その3(3人の相互作用)のグラフで荷重が0に収束しているケースを考察したいのだが各荷重の相互作用があるため変化する荷重が多くて理解しずらいので、変化する荷重を絞った【新】バランス理論の数式表現 その2(自分の評価も考慮)のグラフで、荷重が0に収束しているように見えるケースについて考察する。
荷重が0では好悪感情が無いことになるので、荷重が上記の式(1)~(6)の相互作用の結果として0になることが妥当なのかどうか心配になる。そこで、【新】バランス理論の数式表現 その2(自分の評価も考慮)の次のケースについて考察する。
(【新】バランス理論の数式表現 その2(自分の評価も考慮))
- 図5 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1)
- 図6 Wac(t)、Wbc(t)の変化(Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=1, Wbc(0)=1)
- 図7 Wac(t)、Wbc(t)の変化(Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1)
- 図8 Wac(t)、Wbc(t)の変化(Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1)
- 図10 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1)
- 図12 Wac(t)、Wbc(t)の変化(Waa(0)=1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1)
- 図13 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1)
- 図14 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=1, Wbc(0)=1)
まず、図5、図10、図13、図14は Waa(0)=-1 で図8、図12、図13は Wbb(0)=-1 である。自己評価の荷重がマイナスの場合、上記の通り荷重が収束するのなら0に収束するしかない。荷重が0になって、ようやく安定に近づくことになる。
図6、図7は Waa(0)=1,Wbb(0)=1 で自己評価の荷重がプラスなので、収束した場合に上記の式(14),(16)が成立する。したがって、Wac(t) と Wbc(t) のどちらかが0に収束したらもう一方も0に収束する。
ところで、ハイダーのバランス理論では次の(A)~(F)の不等号が成立すれば安定し、(G)~(L)の不等号が成立している間は不安定である。
\( \begin{cases} W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) > 0\cdots(A)\\ W_{ab}(t) \cdot W_{cb}(t) \cdot W_{ac}(t) > 0\cdots(B)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) > 0\cdots(C)\\ W_{ba}(t) \cdot W_{ca}(t) \cdot W_{bc}(t) > 0\cdots(D)\\ W_{ca}(t) \cdot W_{ab}(t) \cdot W_{cb}(t) > 0\cdots(E)\\ W_{ca}(t) \cdot W_{ba}(t) \cdot W_{cb}(t) > 0\cdots(F)\\ W_{ab}(t) \cdot W_{bc}(t) \cdot W_{ac}(t) < 0\cdots(G)\\ W_{ab}(t) \cdot W_{cb}(t) \cdot W_{ac}(t) < 0\cdots(H)\\ W_{ba}(t) \cdot W_{ac}(t) \cdot W_{bc}(t) < 0\cdots(I)\\ W_{ba}(t) \cdot W_{ca}(t) \cdot W_{bc}(t) < 0\cdots(J)\\ W_{ca}(t) \cdot W_{ab}(t) \cdot W_{cb}(t) < 0\cdots(K)\\ W_{ca}(t) \cdot W_{ba}(t) \cdot W_{cb}(t) < 0\cdots(L)\\ \end{cases} \)
この内の(A),(C)が両立するには、荷重 Wab(t) と Wba(t) の符号が一致しなければいけない。ところが、【新】バランス理論の数式表現 その2(自分の評価も考慮)では Wab(t) と Wba(t) は変化させずに一定にしてあり、図6は Wab(0)=-2, Wba(0)=2 で符号が異なるので、上の(A)と(C)は両立しえない。それで、安定に近づくには Wac(t)×Wbc(t)=0 になるしかない。Wac(t) と Wbc(t) のどちらかが0になるしかないのだが、上記の通り、片方が0に収束したらもう一方も0に収束する。
図7も同様で、Wab(0) と Wba(0) の符号が異なる。したがって、安定に近づいた結果、Wac(t) と Wbc(t) が共に0に収束することになった。
図6も図7も0に収束して安定に近づいたのだが、次の2つは収束せずに不安定なままである。
(【新】バランス理論の数式表現 その2(自分の評価も考慮))
- 図9 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=2, Wac(0)=0, Wba(0)=2, Wbb(0)=-1, Wbc(0)=1)
- 図15 Wac(t)、Wbc(t)の変化(Waa(0)=-1, Wab(0)=-2, Wac(0)=0, Wba(0)=-2, Wbb(0)=-1, Wbc(0)=1)
図9も図15も荷重 Wab(t) と Wba(t) の符号が一致している。しかし、図9を見ると Wac(t)×Wbc(t) は初期状態以外は常にマイナスで、Wab(0) と Wba(0) はプラスで変化させずに一定にしてあるので、3つの荷重の積はマイナスのまま(上の(G)と(I)の不等号)である。そこで図9のように不安定になる。図15は Wac(t)×Wbc(t) は初期状態以外は常にプラスで、Wab(0) と Wba(0) はマイナスで変化させずに一定にしてあるので、3つの荷重の積はマイナスのまま(上の(G)と(I)の不等号)だから不安定になる。
ついでに、【新】バランス理論の数式表現 その2(自分の評価も考慮)の図11を見ると、荷重 Wac(t) と Wbc(t) がそれぞれ別の値に収束している。自己評価の荷重 Waa(t) と Wbb(t) はどちらもプラスで安定しやすい。その他の特徴は Wab(t) と Wba(t) が共にマイナスである。これは Wac(t)×Wbc(t) がマイナスならば、上の(A),(C)が共に成立して安定する。そして、図11を見ると、Wac(t) はマイナスのまま、Wbc(t) はプラスのままだから Wac(t)×Wbc(t) はマイナスのままで、上の(A),(C)が共に成立して安定している。aとbがお互いに嫌っているからcに対する好みも違っている状態である。特にaは最初はcのことを何とも思っていなかったのに、嫌いなbがcのことを好きだからcのことを嫌いになって、そのままという状態である。
最後に、変化する荷重を絞った【新】バランス理論の数式表現 その2(自分の評価も考慮)ではなく、上の式(1)~(6)のままで初期状態を変えて試している際に気になるケースがあったので考察したい。【新】バランス理論の数式表現 その3(3人の相互作用)には載せてない。
初期状態を Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1 にすると、それぞれの荷重は次の図1のように変化する。
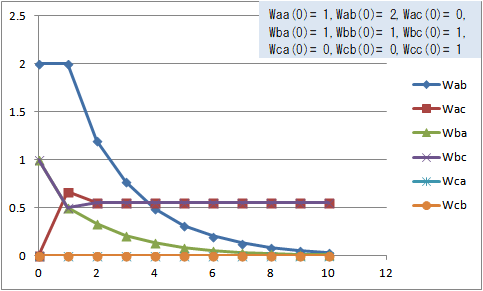
図1 荷重の変化(Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1)
Wab(t) と Wba(t) が0に収束しているのに Wac(t) と Wbc(t) がプラスのまま収束している。
aは最初はcに関心が無かった( Wac(0)=0 )が、好意を寄せているbの影響でcを好きになった。しかし、やがてbへの好意が消失する(Wab(t)=0 )。それでもcを好きな気持ちは変わらなかった。aはbの影響でタレントcを好きになって、bに対する行為が消失してもタレントcのことは好き。そんな状態である。
それでは、なぜaとbはお互いの好意が消失したのだろうか。
それは、cのaやbに対する関心が0のままだからである。これは日常生活でありうるケースである。aやbに対するcの影響を排除しようとして初期状態で Wca(0)=0, Wcb(0)=0 としたのだが、初期状態だけでなく、ずっと Wca(t)=0,Wcb(t)=0 であっても、cのaやbに対する影響は無いとは言えないらしい。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)| }\cdots(1)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)| }\cdots(3)\\ \\ \end{cases} \)
Wca(t)=0, Wcb(t)=0 では式(1),(3)の第2項は0になって、次の式(25),(26)のようになる。
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(25)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(26)\\ \end{cases} \)
式(25),(26)を見るとcの影響が排除されたように見える。しかし、式(25),(26)から次の不等号(27),(28)が成立して荷重 Wab(t) と Wba(t) は0に近づくことになる。
\( \begin{cases} |W_{ab}(t+dt)| < |W_{ab}(t)|\cdots(27)\\ \\ |W_{ba}(t+dt)| < |W_{ba}(t)|\cdots(28)\\ \end{cases} \)
aはbのことが好きだったけれど、bの影響で好きになったcがbに好意を寄せてなかったのでaもbへの好意が薄れていってしまった。そんな感じである。cの影響を排除したつもりだったが、aやbへの無関心が悪影響したような結果になった。
しかし、趣味が同じだったりして好きなものが同じであればお互いに好きになるのが自然ではないだろうか。実は上の式(1)~(6)には、それが反映されてない。
上の式(1)~(6)はハイダーのバランス理論の「好きな人が好きなものだから自分も好き」「好きな人が嫌いなものだから自分も嫌い」「嫌いな人が好きなものだから嫌い」「嫌いな人が嫌いなものだから好き」を数式で表したものである。しかし、ハイダーのバランス理論には「好きなものが同じだから好き」「嫌いなものが同じだから好き」「自分の好きなものを嫌っているから嫌い」「自分の嫌っているものを好きだから嫌い」もある。
次回はハイダーのバランス理論のもう一つの数式表現を提案したい。




コメント 0