【新】バランス理論の数式表現その８（荷重が０になる件の再考察）：【独自研究】ソシオン理論：SSブログ

	ブログをはじめるログイン

【新】バランス理論の数式表現その７（も.. ｜【新】バランス理論の数式表現その９（返.. ブログトップ

【新】バランス理論の数式表現その８（荷重が０になる件の再考察） [編集]

　【新】バランス理論の数式表現その３（３人の相互作用）では、ハイダーのバランス理論を数式表現する際に次の式(1)～(6)を仮定して、各荷重（ Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) ）がどのように変化するかグラフで示した。

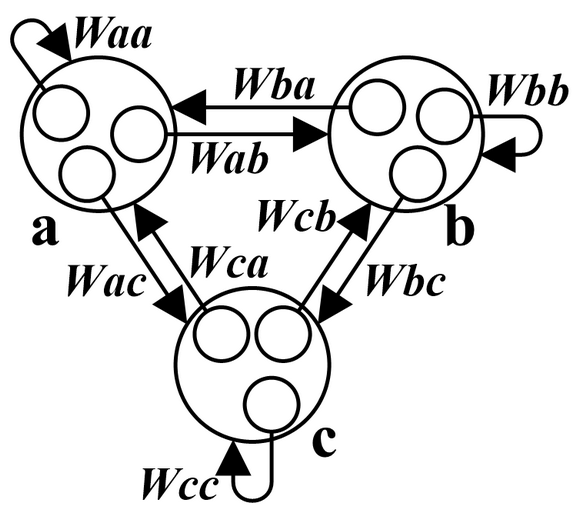
\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(1)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(3)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(5)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(6)\\ \end{cases} \)

　【新】バランス理論の数式表現その７（もう一つの式）では、ハイダーのバランス理論を数式表現する際に次の式(7)～(12)を仮定して、各荷重（ Wab(t), Wac(t), Wba(t), Wbc(t), Wca(t), Wcb(t) ）がどのように変化するかグラフで示した。

\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(7)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{cb}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(8)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(9)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ca}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(10)\\ \\ W_{ca}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{ca}(t) + W_{cb}(t) \cdot W_{ab}(t)}{|W_{cc}(t)| + |W_{cb}(t)|}\cdots(11)\\ \\ W_{cb}(t+dt) =\dfrac{W_{cc}(t) \cdot W_{cb}(t) + W_{ca}(t) \cdot W_{ba}(t)}{|W_{cc}(t)| + |W_{ca}(t)|}\cdots(12)\\ \end{cases} \)

　初期状態を Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1 にすると、それぞれの荷重は式(1)～(6)では次の図１のように変化し、式(7)～(12)では図２のように変化する。

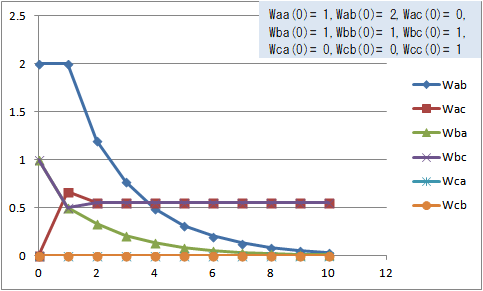
図１式(1)～(6)での荷重の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1）

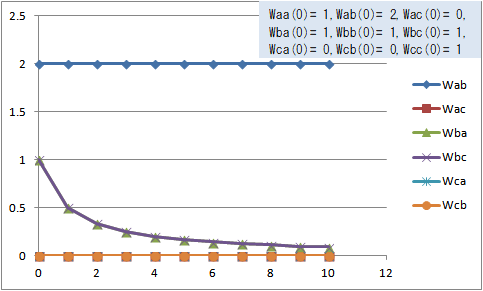
図２式(7)～(12)での荷重の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1）

　ｃの影響を排除するために Wca(0)=0, Wcb(0)=0 としたのだが、式(1)～(6)では Wab(t) と Wba(t) が０に収束し（図１）、式(7)～(12)では Wac(t) が０のままで Wbc(t) は０に収束した（図１）。
　これは、式(1)～(6)、式(7)～(12)は Wca(0)=0, Wcb(0)=0 とすると、次の式(13)～(18)、式(19)～(24)のようになるため、当然の結果である。

\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(13)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(14)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(15)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(16)\\ \\ W_{ca}(t+dt) =W_{ca}(t)=0\cdots(17)\\ \\ W_{cb}(t+dt) =W_{cb}(t)=0\cdots(18)\\ \end{cases} \)

\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(19)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(20)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(21)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(22)\\ \\ W_{ca}(t+dt) =W_{ca}(t)=0\cdots(23)\\ \\ W_{cb}(t+dt) =W_{cb}(t)=0\cdots(24)\\ \end{cases} \)

　式(13)では Wac(t) が０にならない限り、Wab(t+dt) は０に近づく。
　式(15)では Wbc(t) が０にならない限り、Wba(t+dt) は０に近づく。
　式(20)では Wab(t) が０にならない限り、Wac(t+dt) は０に近づく。
　式(22)では Wba(t) が０にならない限り、Wbc(t+dt) は０に近づく。
　そして、Wab(t), Wba(t), Wac(t), Wbc(t) がいったん０になると、Wab(t+dt), Wba(t+dt), Wac(t+dt), Wbc(t+dt) は０のままである。その様子が、図１、図２に現れている。

　問題は、Wca(t)=Wca(0)=0, Wcb(t)=Wcb(0)=0 の時に、式(13)、式(15)、式(20)、式(22)は妥当なのかどうかである。

\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(13)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(15)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(20)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(22)\\ \\ \end{cases} \)

　式(1)は「ａはｃが好き、ｃはｂが好き、だからａはｂが好き」を表した式で、ｃが感情を持たない物や事や架空の存在だったり感情を持っていても好意の返報性が無い相手だった場合には「ｃはｂが好き」が成立しないので「だからａはｂが好き」も成立しない。式(13)は「ａは以前からｂとｃが好き、しかしｃはｂのことが好きでも嫌いでもない、だからａもｂのことが好きでも嫌いでもなくなってくる」という状態を表しているように見える。
　同様に式(3)は「ｂはｃが好き、ｃはａが好き、だからｂはａが好き」を表した式で、「ｃはａが好き」が成立しないので「だからｂはａが好き」も成立しない。式(15)は「ｂは以前からａとｃが好き、しかしｃはａのことが好きでも嫌いでもない、だからｂもａのことが好きでも嫌いでもなくなってくる」という状態を表しているように見える。
　この式(13)と式(15)の解釈は妥当で、実際に起こっていることなのだろうか？
　そもそもａもｂも例えば感情を持たないｃがｂやａに無関心であることは最初から承知していたはずである。それなのに、ｃがｂやａに無関心だからとｂやａのことを好きでも嫌いでもなくなるという、何とも不可解な心理である。

　一方、式(8)は「ａはｂが好き、ｃもｂが好き、だからａはｃが好き」を表した式で、ｃが感情を持たない物や事や架空の存在だったり感情を持っていても好意の返報性が無い相手だった場合には「ｃもｂが好き」が成立しないので「だからａはｃが好き」も成立しない。式(20)は「ａは以前からｂとｃが好き、しかしｃはｂのことが好きでも嫌いでもない、だからａもｃのことが好きでも嫌いでもなくなってくる」という状態を表しているように見える。
　同様に式(10)は「ｂはａが好き、ｃもａが好き、だからｂはｃが好き」を表した式で、「ｃもａが好き」が成立しないので「だからｂはｃが好き」も成立しない。式(22)は「ｂは以前からａとｃが好き、しかしｃはａのことが好きでも嫌いでもない、だからｂもｃのことが好きでも嫌いでもなくなってくる」という状態を表しているように見える。
　この式(20)と式(22)の解釈は妥当で、実際に起こっていることなのだろうか？
　式(8)はｃではなくｂが感情を持たない物や事や架空の存在だったら、式(10)もｃではなくａが感情を持たない物や事や架空の存在だったら、式(20)も式(22)も妥当なように思える。仲良かったのだけど好みの違いが分かって別れる様子を表してる。

　この問題を解決するヒントは【新】バランス理論の数式表現その２（自分の評価も考慮）の図１にあるかもしれない。初期状態の Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1 は上の図１と同じで、Wab(t) と Wba(t) は固定されてる。

\( \begin{cases} W_{ab}(t+dt) =W_{ab}(t)\cdots(13')\\ \\ W_{ba}(t+dt) =W_{ba}(t)\cdots(15')\\ \end{cases} \)

　式(13)を式(13')に、式(15)を式(15')に置き換えてグラフを作成すると、図３のようになる。

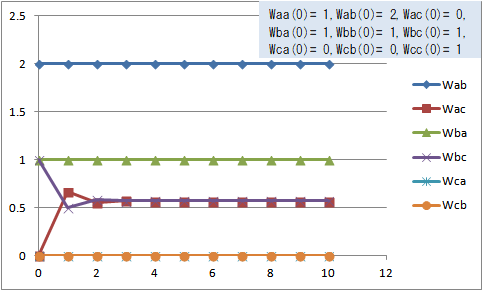
図３式(13'),(14),(15'),(16),(17),(18)での荷重の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1）

　Wac(t) と Wbc(t) の変化は上の図１とほぼ同じである。
　ａ、ｂ、ｃの三者関係でｃが感情を持たない物や事や架空の存在などで Wca(t)=0, Wcb(0)=0 から変わりえない場合は、式(13),(15)、すなわち式(1),(3)を用いてはならず、式(13'),(15')になるような式を用いなければならないのかもしれない。ａやｂが感情を持たない物や事や架空の存在なども同様で、その場合にも問題が生じないように式(1)～(6)を修正しなければならないかもしれない。

　一方、式(20),(22)を次の式(20'),(22')に置き換えてグラフを作成すると、図４のようになる。

\( \begin{cases} W_{ac}(t+dt) =W_{ac}(t)\cdots(20')\\ \\ W_{bc}(t+dt) =W_{bc}(t)\cdots(22')\\ \end{cases} \)

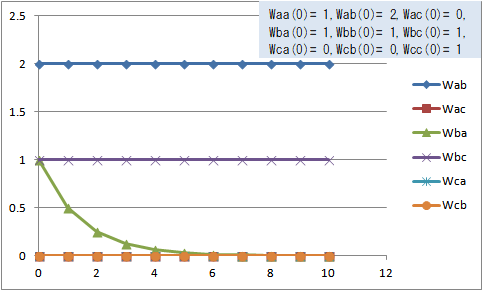
図４式(19),(20'),(21),(22'),(23),(24)での荷重の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1）

　変化したのは Wba(t) だけである。Wba(0)=1 だったが、Wac(t)=Wac(0)=0 で変わらなかったので、Wbc(t)=Wbc(0)=1 のｂはｃに対する好意の違いでａに対する好意が減って Wba(t)=0 に収束した状態である。ただし、ａのｂに対する好意は変わらず Wab(t)=Wab(0)=2 のままである。すなわち、ａとｂは両想いだったが好みの違いでａの片思いになってしまったようなものである。

　では、図３と図４を組み合わせたらどうなるだろうか？
　例えば、図４でａはｂに対して片思いになってしまったが、ａはｂのことが好きだったのだから、ハイダーのバランス理論によれば、ｂの影響でｃが好きになるはずである。それが図３である。その結果、ａの片思いは避けられるはずである。そのような状態を表せる数式はどのようなものだろうか？
　ｃが感情を持たない物や事や架空の存在だったり感情を持っていても好意の返報性が無い相手だった場合に次のようなルールを設けてみる。

\( \begin{cases} W_{ab}(t+dt) ：ａがｂを好きな程度はお互いがｃを好きな程度で変わる\cdots(7)\\ \\ W_{ac}(t+dt) ：ａがｃを好きな程度はｂがｃを好きな程度で変わる\cdots(2)\\ \\ W_{ba}(t+dt) ：ｂがａを好きな程度はお互いがｃを好きな程度で変わる\cdots(9)\\ \\ W_{bc}(t+dt) ：ｂがｃを好きな程度はａがｃを好きな程度で変わる\cdots(4)\\ \\ W_{ca}(t+dt) ：ｃはａに無関心\cdots(17)(23)\\ \\ W_{cb}(t+dt) ：ｃはｂに無関心\cdots(18)(24)\\ \end{cases} \)

　式で表すと次のようになり、それぞれの荷重の変化は図５のようになる。

\( \begin{cases} W_{ab}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ab}(t) + W_{ac}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ac}(t)|}\cdots(7)\\ \\ W_{ac}(t+dt) =\dfrac{W_{aa}(t) \cdot W_{ac}(t) + W_{ab}(t) \cdot W_{bc}(t)}{|W_{aa}(t)| + |W_{ab}(t)|}\cdots(2)\\ \\ W_{ba}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{ba}(t) + W_{bc}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{bc}(t)|}\cdots(9)\\ \\ W_{bc}(t+dt) =\dfrac{W_{bb}(t) \cdot W_{bc}(t) + W_{ba}(t) \cdot W_{ac}(t)}{|W_{bb}(t)| + |W_{ba}(t)|}\cdots(4)\\ \\ W_{ca}(t+dt) =W_{ca}(t)=0\cdots(17)\\ \\ W_{cb}(t+dt) =W_{cb}(t)=0\cdots(18)\\ \end{cases} \)

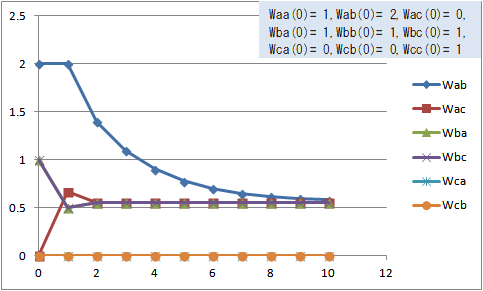
図５式(7),(2),(9),(4),(17),(18)での荷重の変化（Waa(0)=1, Wab(0)=2, Wac(0)=0, Wba(0)=1, Wbb(0)=1, Wbc(0)=1, Wca(0)=0, Wcb(0)=0, Wcc(0)=1）

　図５は頷ける結果である。問題は式(1)～(6)と式(7)～(12)を組み合わせて図５のような妥当な結果になるような数式を作ることである。

　ｃの影響を排除するために Wca(0)=0, Wcb(0)=0 にすると、図１、図２のような結果になってしまった問題を解決するヒントは【ソシオン理論の表記法】に書いた次の部分にもある。

　さて、b は a が好き（Wba ＞ 0）だが、a は b に嫌われている（Wba ＜ 0）と思っていることがあるだろう。そして、a の行動は事実よりも a の主観に基づいて決まる。したがってネットワーク上の各自の主観を考察するための表記が必要である。
　このブログでは a が思っている「b の a に対する評価」を Wba|a と書くことにする。同様に b が思っている「a の b に対する評価」を Wab|b と書く。他にも a が思っている「b の自分に対する評価」を Wbb|a、 b が思っている「a の自分に対する評価」を Waa|b と書く。一般に i が思っている「j の k に対する評価」を Wjk|i と書くことにする。
　「 b は a が好き」は「Wba|b ＞ 0」であり、「 a が b に嫌われていると思っている」状態は「Wba|a ＜ 0」である。「 a が b に好かれていると思っている」状態は「Wba|a ＞ 0」である。
（ソシオン理論の表記法）

　このことを踏まえて式(1)～(6)と式(7)～(12)を書き換えると次の式(1')～(6')と式(7')～(12')になる。

\( \begin{cases} W_{ab|a}(t+dt) =\dfrac{W_{aa|a}(t) \cdot W_{ab|a}(t) + W_{ac|a}(t) \cdot W_{cb|a}(t)}{|W_{aa|a}(t)| + |W_{ac|a}(t)|}\cdots(1')\\ \\ W_{ac|a}(t+dt) =\dfrac{W_{aa|a}(t) \cdot W_{ac|a}(t) + W_{ab|a}(t) \cdot W_{bc|a}(t)}{|W_{aa|a}(t)| + |W_{ab|a}(t)|}\cdots(2')\\ \\ W_{ba|b}(t+dt) =\dfrac{W_{bb|b}(t) \cdot W_{ba|b}(t) + W_{bc|b}(t) \cdot W_{ca|b}(t)}{|W_{bb|b}(t)| + |W_{bc|b}(t)|}\cdots(3')\\ \\ W_{bc|b}(t+dt) =\dfrac{W_{bb|b}(t) \cdot W_{bc|b}(t) + W_{ba|b}(t) \cdot W_{ac|b}(t)}{|W_{bb|b}(t)| + |W_{ba|b}(t)|}\cdots(4')\\ \\ W_{ca|c}(t+dt) =\dfrac{W_{cc|c}(t) \cdot W_{ca|c}(t) + W_{cb|c}(t) \cdot W_{ba|c}(t)}{|W_{cc|c}(t)| + |W_{cb|c}(t)|}\cdots(5')\\ \\ W_{cb|c}(t+dt) =\dfrac{W_{cc|c}(t) \cdot W_{cb|c}(t) + W_{ca|c}(t) \cdot W_{ab|c}(t)}{|W_{cc|c}(t)| + |W_{ca|c}(t)|}\cdots(6')\\ \end{cases} \)

\( \begin{cases} W_{ab|a}(t+dt) =\dfrac{W_{aa|a}(t) \cdot W_{ab|a}(t) + W_{ac|a}(t) \cdot W_{bc|a}(t)}{|W_{aa|a}(t)| + |W_{ac|a}(t)|}\cdots(7')\\ \\ W_{ac|a}(t+dt) =\dfrac{W_{aa|a}(t) \cdot W_{ac|a}(t) + W_{ab|a}(t) \cdot W_{cb|a}(t)}{|W_{aa|a}(t)| + |W_{ab|a}(t)|}\cdots(8')\\ \\ W_{ba|b}(t+dt) =\dfrac{W_{bb|b}(t) \cdot W_{ba|b}(t) + W_{bc|b}(t) \cdot W_{ac|b}(t)}{|W_{bb|b}(t)| + |W_{bc|b}(t)|}\cdots(9')\\ \\ W_{bc|b}(t+dt) =\dfrac{W_{bb|b}(t) \cdot W_{bc|b}(t) + W_{ba|b}(t) \cdot W_{ca|b}(t)}{|W_{bb|b}(t)| + |W_{ba|b}(t)|}\cdots(10')\\ \\ W_{ca|c}(t+dt) =\dfrac{W_{cc|c}(t) \cdot W_{ca|c}(t) + W_{cb|c}(t) \cdot W_{ab|c}(t)}{|W_{cc|c}(t)| + |W_{cb|c}(t)|}\cdots(11')\\ \\ W_{cb|c}(t+dt) =\dfrac{W_{cc|c}(t) \cdot W_{cb|c}(t) + W_{ca|c}(t) \cdot W_{ba|c}(t)}{|W_{cc|c}(t)| + |W_{ca|c}(t)|}\cdots(12')\\ \end{cases} \)

　式(1')～(6')と式(7')～(12')は次のような表記の方が良いかもしれないが、ここでは引用しやすくするために上の表記を使う。

\( \begin{cases} W^a_{ab}(t+dt) =\dfrac{W^a_{aa}(t) \cdot W^a_{ab}(t) + W^a_{ac}(t) \cdot W^a_{cb}(t)}{|W^a_{aa}(t)| + |W^a_{ac}(t)|}\cdots(1')\\ \\ W^a_{ac}(t+dt) =\dfrac{W^a_{aa}(t) \cdot W^a_{ac}(t) + W^a_{ab}(t) \cdot W^a_{bc}(t)}{|W^a_{aa}(t)| + |W^a_{ab}(t)|}\cdots(2')\\ \\ W^b_{ba}(t+dt) =\dfrac{W^b_{bb}(t) \cdot W^b_{ba}(t) + W^b_{bc}(t) \cdot W^b_{ca}(t)}{|W^b_{bb}(t)| + |W^b_{bc}(t)|}\cdots(3')\\ \\ W^b_{bc}(t+dt) =\dfrac{W^b_{bb}(t) \cdot W^b_{bc}(t) + W^b_{ba}(t) \cdot W^b_{ac}(t)}{|W^b_{bb}(t)| + |W^b_{ba}(t)|}\cdots(4')\\ \\ W^c_{ca}(t+dt) =\dfrac{W^c_{cc}(t) \cdot W^c_{ca}(t) + W^c_{cb}(t) \cdot W^c_{ba}(t)}{|W^c_{cc}(t)| + |W^c_{cb}(t)|}\cdots(5')\\ \\ W^c_{cb}(t+dt) =\dfrac{W^c_{cc}(t) \cdot W^c_{cb}(t) + W^c_{ca}(t) \cdot W^c_{ab}(t)}{|W^c_{cc}(t)| + |W^c_{ca}(t)|}\cdots(6')\\ \end{cases} \)

\( \begin{cases} W^a_{ab}(t+dt) =\dfrac{W^a_{aa}(t) \cdot W^a_{ab}(t) + W^a_{ac}(t) \cdot W^a_{bc}(t)}{|W^a_{aa}(t)| + |W^a_{ac}(t)|}\cdots(7')\\ \\ W^a_{ac}(t+dt) =\dfrac{W^a_{aa}(t) \cdot W^a_{ac}(t) + W^a_{ab}(t) \cdot W^a_{cb}(t)}{|W^a_{aa}(t)| + |W^a_{ab}(t)|}\cdots(8')\\ \\ W^b_{ba}(t+dt) =\dfrac{W^b_{bb}(t) \cdot W^b_{ba}(t) + W^b_{bc}(t) \cdot W^b_{ac}(t)}{|W^b_{bb}(t)| + |W^b_{bc}(t)|}\cdots(9')\\ \\ W^b_{bc}(t+dt) =\dfrac{W^b_{bb}(t) \cdot W^b_{bc}(t) + W^b_{ba}(t) \cdot W^b_{ca}(t)}{|W^b_{bb}(t)| + |W^b_{ba}(t)|}\cdots(10')\\ \\ W^c_{ca}(t+dt) =\dfrac{W^c_{cc}(t) \cdot W^c_{ca}(t) + W^c_{cb}(t) \cdot W^c_{ab}(t)}{|W^c_{cc}(t)| + |W^c_{cb}(t)|}\cdots(11')\\ \\ W^c_{cb}(t+dt) =\dfrac{W^c_{cc}(t) \cdot W^c_{cb}(t) + W^c_{ca}(t) \cdot W^c_{ba}(t)}{|W^c_{cc}(t)| + |W^c_{ca}(t)|}\cdots(12')\\ \end{cases} \)

　例えば、Wac|a(t) と Wac|b(t) は同じであるとは限らない。図１は式(1)と式(4)の Wac(t) を同じ値にして得られたグラフであるが、式(1')と式(4')のように異なる値を用いるべきかもしれず、図２は式(7)と式(9)の Wac(t) を同じ値にして得られたグラフであるが、式(7')と式(4')のように異なる値を用いるべきかもしれない。他の荷重についても同様である。

\( \begin{cases} W_{ab|a}(t) = W_{ab|b}(t) = W_{ab|c}(t) = W_{ab}(t)\\ \\ W_{ac|a}(t) = W_{ac|b}(t) = W_{ac|c}(t) = W_{ac}(t)\\ \\ W_{ba|a}(t) = W_{ba|b}(t) = W_{ba|c}(t) = W_{ba}(t)\\ \\ W_{bc|a}(t) = W_{bc|b}(t) = W_{bc|c}(t) = W_{bc}(t)\\ \\ W_{ca|a}(t) = W_{ca|b}(t) = W_{ac|a}(t) = W_{ac}(t)\\ \\ W_{cb|a}(t) = W_{cb|b}(t) = W_{bc|b}(t) = W_{bc}(t)\\ \\ W_{ca|c}(t) = W_{ca}(t) = 0\\ \\ W_{cb|c}(t) = W_{cb}(t) = 0\\ \end{cases} \)

　上の仮定は客観的にはａやｂに無関心なｃの好悪感情（ Wca=0, Wcb=0 ）を好意の返報性が生じている（ Wca=Wac, Wcb=Wbc ）かのようにａとｂが勘違いしてる状態である。

　図５と同じ結果になったのは、上の仮定を式(1')～(6')と式(7')～(12')に代入した結果を式(7),(2),(9),(4),(17),(18)と比べてみれば、当然であることが分かる。しかし、上の仮定はｃの好悪感情以外を客観的な好悪感情に一致させていて現実的ではないような気がするし、ａやｂが想像してるｃの好悪感情も特殊な設定である。今後も続けて同じような仮定で進めない方が良いかもしれない。
　客観的な好悪感情ではなく主観的な好悪感情で数式にした式(1')～(6')と式(7')～(12')は初期状態を設定する荷重が(1)～(6)と式(7)～(12)の場合の３倍近くになる。また、好悪感情の変化をシミュレートするにはそれぞれの主観的な好悪感情を結び付ける数式も必要である。したがって、主観的な好悪感情を結び付ける数式が思いつくまでは、主観的な好悪感情が客観的な好悪感情と一致する仮定でシミュレートするしかないだろう。