【新】バランス理論の数式表現 その1(単純な積ではダメ)
2008年に書いた【バランス理論の数式表現】では難しく考えすぎていて、さらに【荷重の大きさを1以下にする工夫】で次のような制限を入れたために【最終的に荷重が0になってしまう異常】のようになってしまい、いったんは挫折した。
ソシオン理論の荷重には次のような制限があるらしい。
−1 ≦ Wab ≦ 1 ・・・(1)
このような制限が必要な理由は分からないが、もしも制限が必要ならば数式を使って荷重の値を求めた結果も(1)の範囲内に収まる必要がある。
(荷重の大きさを1以下にする工夫)
ここからは、これまでの思考をリセットして、「−1 ≦ Wab ≦ 1」の制限も無視して、改めてハイダーのバランス理論を数式で表現することに挑戦したい。既に誰かが論文などにしているかもしれないが、私は読んでいないので、自分の頭でこれまでの知識を基に一から考えたい。
まずは単純な発想から。
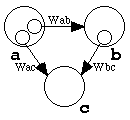
図1 基本の図
aのcに対する評価は少し前(dt時間前)aのbに対する評価とbのcに対する評価の積で決まると仮定してみる。すると、どのようなことが起こるであろうか。
Wab(0) = 2
Wbc(0) = 1
Wac(0) = 0
このように初期状態を入力すると、(1)の結果、次のようになって安定する。
Wab(t) = 2
Wbc(t) = 1
Wac(t) = 2
しかし、bにもハイダーのバランス理論が適用されて、aのcに対する評価に影響されるはずである。
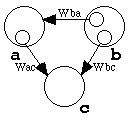
図2 bのaやcに対する評価
その結果、Wab(0) = 2, Wbc(0) = 1, Wac(0) = 0 から始まって、次に Wac(1) = 2 となって想定通りでも、例えば Wba(0) = 1 なら Wbc(1) = 0にもなる。その結果、その次は Wac(2) = 0, Wbc(2) = 2 になる。さらに、その次は Wac(3) = 4, Wbc(3) = 0 になって不安定である。
グラフにすると次のようになる。
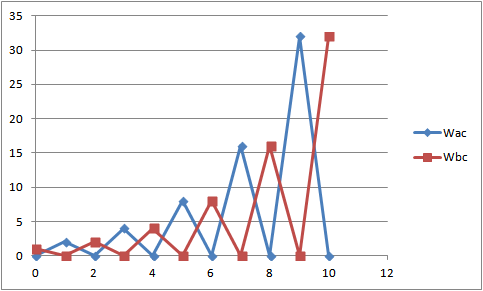
図3 ハイダーのバランス理論を単純な積で表現した場合の評価の揺らぎ。
ちなみに、初期状態を Wab(0) = 2, Wbc(0) = 1, Wac(0) = 1, Wba(0) = 1 に変えると次のようになる。
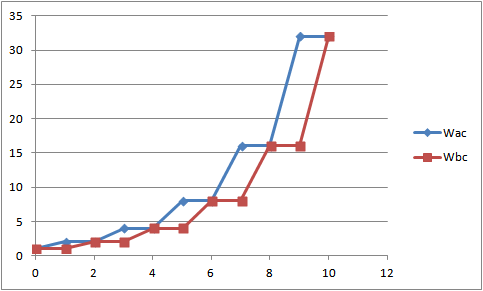
図4 ハイダーのバランス理論を単純な積で表現した場合の評価の鰻上り。
(1)や(2)のように単純な積で表現してはだめなことが分かった。
そもそも、何かを評価する時、自分がもともと持っていた評価を無視して他の人の評価だけに影響されてはダメだろう。そこで、もともとの自分の評価も考慮するために、自分自身に対する評価 Waa(t) , Wbb(t) を使って、Waa(t)・Wac(t) , Wbb(t)・Wbc(t) も数式に入れてみようと思う。その際に、 Wac(t) , Wbc(t) が安定するように作らないといけないが、それは次回。
最終的に荷重が0になってしまう異常
次の3式を前提に考えてみる。
-1 ≦ Wij ≦ 1 ・・・(1)
| n | |||||||
| Waa|a | = | η | ∑ | [f(Wai|a) | ・ | g(Wia|a)] | ・・・(2) |
| i=1 | |||||||
| n | |||||||
| Wab|a | = | η | ∑ | [f(Wai|a) | ・ | g(Wib|a)] | ・・・(3) |
| i=1 | |||||||
例えば式(3)で「n=1」の場合は三者だけの関係を表す式であり、次の式(4)のように書き換えた方が分かりやすい。
Wab|a = η・f(Wac|a)・g(Wcb|a) ・・・(4)
ηがどのような値で、f(Wac|a)やg(Wcb|a)がどのような関数かはまだ分からない。分からないが式(4)で荷重 Wab|a を求めるときに気になることがある。それは以下のように「1以下の正の数に1以下の正の数を掛けると元の数よりも小さくなる」ということである。
「0 ≦ Wac|a ≦ 1」で「0 ≦ f(Wac|a) ≦ 1」 ・・・(5)
「0 ≦ Wcb|a ≦ 1」で「0 ≦ g(Wcb|a) ≦ 1」 ・・・(6)
「(5)かつ(6)」ならば「0 ≦ f(Wac|a)・g(Wcb|a) ≦ f(Wac|a)」 ・・・(7)
「(5)かつ(6)」ならば「0 ≦ f(Wac|a)・g(Wcb|a) ≦ g(Wcb|a)」 ・・・(8)
「η≦1」ならば(7)(8)は次のようになる。
「(5)かつ(6)」ならば「0 ≦ Wab|a ≦ f(Wac|a)」 ・・・(9)
「(5)かつ(6)」ならば「0 ≦ Wab|a ≦ g(Wcb|a)」 ・・・(10)
ここで、もしも「f(Wac|a) ≦ Wac|a」「g(Wcb|a) ≦ Wcb|a」ならば(9)(10)は次のようになる。
「(5)かつ(6)」ならば「0 ≦ Wab|a ≦ Wac|a」 ・・・(11)
「(5)かつ(6)」ならば「0 ≦ Wab|a ≦ Wcb|a」 ・・・(12)
「f(Wac|a) > Wac|a」「g(Wcb|a) > Wcb|a」であっても(11)(12)は起こりやすい。
f(Wac|a)・g(Wcb|a) = 0.2×0.4 = 0.08
Wab|a = η・f(Wac|a)・g(Wcb|a) = 0.08
∴ 0 ≦ Wab|a ≦ Wac|a,0 ≦ Wab|a ≦ Wcb|a
(11)は「 c のことが好きだから c が好いている b のことも好きになったが、b への好意は c への好意よりも強くなることはない」ということで、(12)は「 c のことが好きだから c が好いている b のことも好きになったが、b への好意は c の b への好意よりも強くなることはない」ということだろう。b に「音楽」を当てはめると「あなたが音楽を好きだから私も音楽が好きになったけれど、私はあなたほど音楽を愛せないし、私は音楽よりもあなたの方が好き」ということだろう。「私」が「あなた」よりも「音楽」を好きになるには「あなた」や「音楽」との三者関係だけでは無理で、他の人との関係で「音楽」への好意を加算しなければいけないということだろう。
このように書くともっともらしいのだが、次の式(13)を加えると単純に考えられそうにない。
Wac|a = η・f(Wab|a)・g(Wbc|a) ・・・(13)
式(4)から(11)(12)に至ったように、次の(5’)(6’)を前提にすると、式(13)から次の(14)(15)が得られる。
「0 ≦ Wab|a ≦ 1」で「0 ≦ f(Wab|a) ≦ 1」 ・・・(5’)
「0 ≦ Wbc|a ≦ 1」で「0 ≦ g(Wbc|a) ≦ 1」 ・・・(6’)
「(5’)かつ(6’)」ならば「0 ≦ Wac|a ≦ Wab|a」 ・・・(14)
「(5’)かつ(6’)」ならば「0 ≦ Wac|a ≦ Wbc|a」 ・・・(15)
f(Wab|a)・g(Wbc|a) = 0.16×0.4 = 0.064
Wac|a = η・f(Wab|a)・g(Wbc|a) = 0.064
∴ 0 ≦ Wac|a ≦ Wab|a,0 ≦ Wac|a ≦ Wbc|a
f(Wac|a)・g(Wcb|a) = 0.128×0.4 = 0.0512
Wab|a = η・f(Wac|a)・g(Wcb|a) = 0.0512
∴ 0 ≦ Wab|a ≦ Wac|a,0 ≦ Wab|a ≦ Wcb|a
(11)と(14)がほぼ矛盾してしまう。矛盾しないのは「Wab|a = Wac|a」になったときだけである。時間軸を用意し、(11)と(14)を交互に繰り返すと、最終的に「Wab|a = Wac|a = 0」になってしまう。これをどのように解釈したら良いのだろうか。「-1 ≦ Wac|a ≦ 0」「-1 ≦ Wcb|a ≦ 0」「-1 ≦ Wab|a ≦ 0」「-1 ≦ Wbc|a ≦ 0」の場合は、さらに異常な結論が得られそうである。
【バランス理論の数式表現】の終わりの方にも書いたが、荷重を求める数式に利用する関数 f(x) や g(x) を選択する際には、異常な結論が得られないように注意が必要である。実際に数値を当てはめてシミュレーションしたら、異常な解釈しかできない結果になってないか、また、当てはめる数値を多様にしたら異常な結果が得られないか、慎重に検討する必要がある。
追記:
(5)(6)(5’)(6’)の「で」の前は不要かもしれないが、関数 f(x) や g(x) が1以下になりやすく、異常が起こりやすいということで…。
荷重の大きさを1以下にする工夫
ソシオン理論の荷重には次のような制限があるらしい。
−1 ≦ Wab ≦ 1 ・・・(1)
このような制限が必要な理由は分からないが、もしも制限が必要ならば数式を使って荷重の値を求めた結果も(1)の範囲内に収まる必要がある。注意が必要なのは、自己評価やハイダーのバランス理論において複数の荷重を足し合わせる場合である。
例えば、自己評価を表す荷重(Waa|a)を複数の他者(1 〜 n)からの評価(荷重 Wia|a)を使って求める数式は次のように表現できる(参照)。
| n | |||||||
| Waa|a | = | η | ∑ | [f(Wai|a) | ・ | g(Wia|a)] | ・・・(2) |
| i=1 | |||||||
また、他者(b)に対する荷重(Wab|a)をハイダーのバランス理論を使って複数の他者(1 〜 n)の b に対する荷重(Wib|a)から求める数式は次のように表現できる(参照)。
| n | ||
| Wab|a = η | ∑ | [f(Wai|a)・g(Wib|a)] ・・・(3) |
| i=1 |
式(2)や式(3)のように加算を繰り返してnが大きくなれば、通常は(1)の範囲内に収まらない。(1)の範囲に収めるには何らかの工夫が必要である。
まずは、「−1 ≦ y ≦ 1」となる関数を探す。
例えば次の数式の y は x がどんな値でも「−1 ≦ y ≦ 1」となる。
| y = (2/π) tan-1(x) = (2/π) arctan(x) | ・・・(4) |
| y = erf(x) | ・・・(5) |
| y = sgn(x)√(1 − exp(-4x2/π)) | ・・・(5’) |
| y = sgn(x)(1 − exp(-4x2/π)) | ・・・(6) |
式(5)は誤差関数と呼ばれ、式(5’)で近似できる(参照)。式(5’)(6)の sgn(x) は符号関数である。
式(4)(5’)(6)をグラフにすると、図1のようになる。
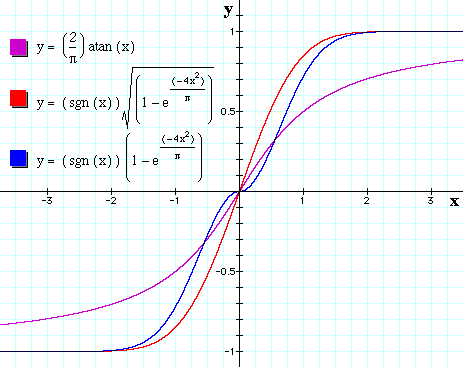 |
図1 |
グラフの傾きを変えたい場合は、式(4)(5’)(6)を次のように変える。
| y = (2/π) tan-1(αx) = (2/π) arctan(αx) | ・・・(7) |
| y = sgn(x)√(1 − exp(-αx2)) | ・・・(8) |
| y = sgn(x)(1 − exp(-αx2)) | ・・・(9) |
例えば式(8)のαを変えてグラフにすると、図2のようになる。
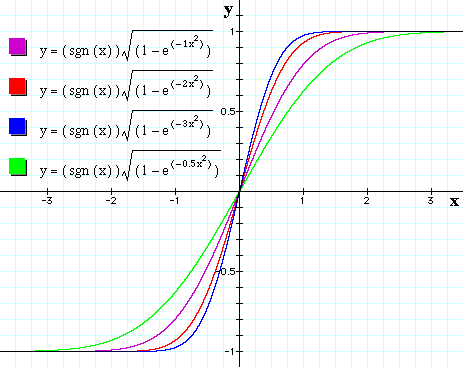 |
図2 |
式(4)〜(9)は(1)の範囲に収まるが、式(2)や式(3)の加算する前の f(Wai|a) や g(Wib|a) に式(4)〜(9)を用いると、加算する荷重の数(n)が大きくなると(1)の範囲に収まらなくなってしまう。そこで、式(2)の Waa|a や式(3)の Wab|a の部分を式(4)〜(9)の x として式(4)〜(9)の y を Waa|a や Wab|a にする。
例えば式(8)を使うとして、次のようにする。
| n | |||||||
| xaa | = | η | ∑ | [f(Wai|a) | ・ | g(Wia|a)] | ・・・(10) |
| i=1 | |||||||
| n | |||||||
| xab | = | η | ∑ | [f(Wai|a) | ・ | g(Wib|a)] | ・・・(11) |
| i=1 | |||||||
| Waa|a = sgn(xaa)√(1 − exp(-αxaa2)) | ・・・(12) |
| Wab|a = sgn(xab)√(1 − exp(-αxab2)) | ・・・(13) |
このような工夫で荷重を(1)の範囲に収めることができる。
【追記(2008/11/10)】自己評価の決まり方
【自己評価の決まり方】に次の記述を追加した。
追記(2008/11/10):
式(5)は式(2)(2’)(2'')を一般化したのでΔWaa|a を求める式になっているが、Waa|a を求める次の式(6)の方が良いかもしれない。
Waa|a = η・f(Wab|a)・g(Wba|a) ・・・(6)
式(6)を基にした場合、Waa|a を求めるために使われている g(Wba|a) と同じ関数を g(ΔWba|a) として式(5)のようにΔWaa|a を求める際に使えるとは限らないので注意が必要である。 Wab|a が変化しなければ次のように求めることになる。
ΔWaa|a = η・f(Wab|a)・[ g(Wba|a+ΔWba|a) - g(Wba|a) ] ・・・(5’)
b からの評価(Wba|a)が変化した後と変化する前の自己評価(Waa|a)の差がΔWaa|a である。「Wba|a = 0 かつ g(Wba|a) = 0」の時に、すなわち、初めて b から評価された場合は式(5)になるが、「ΔWba|a = Wba|a」と見なせるので、次の式(5'')になる。
ΔWaa|a = η・f(Wab|a)・g(Wba|a) ・・・(5'')
また、b 以外からの評価を含めた一般式は次のようになる。
Waa|a = η・[ f(Wa1|a)・g(W1a|a) + f(Wa2|a)・g(W2a|a) + f(Wa3|a)・g(W3a|a) +…+ f(Wan|a)・g(Wna|a) ] ・・・(7)
W1a|a ~ Wna|a の一つだけが変化した場合のΔWaa|a は式(5’)のように求める。



